黄博士网: 教育网, AI数学手册计算器软件，电化学虚拟实验室，虚拟电化学工作站，电化学软件
首页
| 目录
| 世界
| 学科
| 文科
| 科学
| 数学
| 物理
| 化学
| 医学
| 计算
| 软件
| 帮助
| 打赏
+ 
+ 
+ 
= 
反函数
设函数 y=f(x)(x∈A) 的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作y=f^(-1)(x) 。反函数y=f ^(-1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域。
最具有代表性的反函数就是对数函数与指数函数。
一般地，如果x与y关于某种对应关系f（x）相对应，y=f（x），则y=f（x）的反函数为x=f (y)或者y=f﹣¹（x）。
存在反函数(默认为单值函数）的条件是原函数必须是一一对应的（不一定是整个数域内的）。注意：上标"−1"指的并不是幂。
定义
设函数y=f(x) 的
定义域是D，
值域是f(D)。如果对于值域f(D)中的每一个y，在D中有且只有一个x使得g(y)=x，则按此对应法则得到了一个定义在f(D)上的函数，并把该函数称为函数y=f(x) 的
反函数，
记为
f
-1(x)
由该定义可以很快得出函数f(x) 的定义域D和值域f(D)恰好就是反函数 f-1(x) 的值域和定义域，并且f-1(x) 的反函数就是f(x)，也就是说，
函数f(x) 和f-1(x) 互为反函数，即：
inverse(f(x)) = f-1(x)
反函数与原函数的复合函数等于x，即：
f-1(f(x)) = x
习惯上我们用x来表示
自变量，用y来表示
因变量，于是函数y=f(x) 的反函数通常写成
f-1(x)
。
例如，函数
exp(x)
的反函数是
log(x)
。
相对于反函数y=f-1(x) 来说，原来的函数y=f(x) 称为直接函数。反函数和直接函数的图像关于直线y=x对称。这是因为，如果设(a,b)是y=f(x) 的图像上任意一点，即b=f(a)。根据反函数的定义，有a=f-1(b)，即点(b,a)在反函数y=f-1(x) 的图像上。而点(a,b)和(b,a)关于直线y=x对称，由(a,b)的任意性可知f和f-1关于y=x对称。
于是我们可以知道，如果两个函数的图像关于y=x对称，那么这两个函数互为反函数。这也可以看做是反函数的一个几何定义。
在微积分里，
f (n)(
x)是用来指
f的n次
微分的。
若一函数有反函数，此函数便称为
可逆的（invertible）。
[1]
反函数存在性
反函数概述
一函数
f若要是一明确的反函数，它必须是一
双射函数，即：
（
单射）
陪域上的每一元素都必须只被
f映射到一次：不然其反函数将必须将元素映射到超过一个的值上去。
（
满射）陪域上的每一元素都必须被
f映射到：不然将没有办法对某些元素定义
f的反函数。
若
f为一
实变函数，则若
f有一明确反函数，它必通过水平线测试，即一放在
f图上的水平线
必对所有实数
k，通过且只通过一次。
[1]
反函数存在定理
定理：严格
单调函数必定有严格单调的反函数，并且二者单调性相同。
在证明这个定理之前先介绍函数的严格单调性。
设y=f(x) 的
定义域为D，
值域为f(D)。如果对D中任意两点x
1和x
2，当x
1<x
2时，有y
1<y
2，则称y=f(x) 在D上严格单调递增；当x
1<x
2时，有y
1>y
2，则称y=f(x) 在D上严格单调递减。
证明：设f在D上严格单增，对任一y∈f(D)，有x∈D使f(x) =y。
而由于f的严格单增性，对D中任一x'<x，都有y'<y；任一x''>x，都有y''>y。总之能使f(x) =y的x只有一个，根据反函数的定义，f存在反函数f-1。
任取f(D)中的两点y1和y2，设y1<y2。而因为f存在反函数f-1，所以有x1=f-1(y1)，x2=f-1(y2)，且x1、x2∈D。
若此时x1≥x2，根据f的严格单增性，有y1≥y2，这和我们假设的y1<y2矛盾。
因此x1<x2，即当y1<y2时，有f-1(y1)<f-1(y2)。这就证明了反函数f-1也是严格单增的。
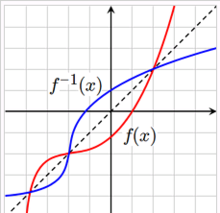函数及其反函数的图形关于直线y=x对称
exp(x) 的反函数 =
inverse(exp(x))
sin(x) 的反函数 =
inverse(y=sin(x))
性质
（2）一个函数与它的反函数在相应
区间上
单调性一致；
（3）大部分
偶函数不存在反函数（当函数y=f(x)， 定义域是{0} 且 f(x)=C （其中C是常数），则函数f(x) 是偶函数且有反函数，其反函数的定义域是{C}，值域为{0} ）。
奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数。若一个
奇函数存在反函数，则它的反函数也是奇函数。
（4）一段连续的函数的单调性在对应区间内具有一致性；
（5）严增（减）的函数一定有严格增（减）的反函数；
（6）反函数是相互的且具有唯一性；
（8）反函数的
导数关系：如果x=f(y)在开区间I上严格单调，可导，且f'(y)≠0，那么它的反函数y=f
-1(x) 在区间S={x|x=f(y),y∈I }内也可导，且：
(10) 函数及其反函数的图形关于直线 y=x 对称.
反函数的符号
反函数的符号记为f
-1(x)，在中国的教材里，
反三角函数记为arcsin、arccos等等，但是在欧美一些国家，sin(x) 的反函数记为sin
-1(x)。
x-1表示1/x，那么f-1(x) 与这是否有些关系呢？下面举几个例子来说明这点。当然，f-1(x) 肯定和1/f(x) 不等，但是确实有与之很相近的性质。
（1）反函数的反函数
为了好看以及对比，我有时会把f(x) 写成f对比，我把我想各位应该很好理解，反函数的反函数当然就是原函数，写成数学语言就是(f
-1)
-1=f。看看，这是不是有点像
指数的运算法则：1/x
-1=x呢？
（2）反函数的导函数
如果函数x=f(y)在区间Iy内单调、可导且f '(y)不等于零，则它的反函数y=f
-1(x) 在区间
内也可导，且
或
。
[2]
用自然语言来说就是，反函数的
导数，等于直接函数导数的倒数。这话有点绕，不过应该能读懂，这个似乎就进一步揭示了反函数符号的意义。
在这里要说明的是，y=f(x) 的反函数应该是x=f
-1(y)。只不过在通常的情况下，我们将x写作y，y写作x，以符合习惯。所以，虽然反函数和直接函数不互为
倒数，但是各自导函数求出后，二者却是互为倒数。
（3）反函数的复合函数
这个内容属于高等数学的内容了。大伙想想函数里面最简单最基本的函数是什么函数？不用说，肯定就是我们的
恒等函数y=x，这就和我们数字里面的1一般地位，所以，我们记恒等函数为“1
x”。
数字的基本运算就是加减乘除，而函数也有运算，虽然也有加减乘除，但是属于函数自己的，就是复合与反函数。我们知道在实数里，x与1/x的乘积等于1，在函数的复合运算里，也有类似的性质，函数f和g的复合记为f○g，那么下面的性质成立：f-1○f=1x；1x○f=f○1x=f。
这第一个式子已经说明很多问题。实际上，这些都是属于
高等代数的内容，在每一个封闭的系统里，都有一个“单位1”，都有自己的运算法则，函数里的就是1
x，实数里的就是数字1等等。要深刻理解这些，也只有大家接触群论以后才会深入理解。这里也只是做点皮毛而已。我将在后面另起一文，介绍函数的“幂”的概念，就如同数的幂一样。
[3]
说明
（1）在函数x=f
-1(y)中，y是
自变量，x是
函数，但习惯上，我们一般用x表示自变量，用y 表示函数，为此我们常常对调函数x=f
-1(y)中的字母x,y，把它改写成y=f
-1(x)，今后凡无特别说明，函数y=f(x) 的反函数都采用这种经过改写的形式。
(2) 反函数也是函数，因为它符合函数的定义. 从反函数的定义可知，对于任意一个函数y=f(x) 来说，不一定有反函数，若函数y=f(x) 有反函数y=f -1(x)，那么函数y=f -1(x) 的反函数就是y=f(x)，这就是说，函数y=f(x) 与y=f -1(x) 互为反函数。
(3) 互为反函数的两个函数在各自定义域内有相同的单调性。
单调函数一定有反函数，如
二次函数在R内不是反函数，但在其单调增（减）的定义域内，可以求反函数；另外，
反比例函数等函数不单调，也可求反函数。
(4) 从
映射的
定义可知，函数y=f(x) 是定义域A到值域C的映射，而它的反函数y=f
-1(x) 是集合C到集合A的映射，因此，函数y=f(x) 的定义域正好是它的反函数y=f
-1(x) 的值域；函数y=f(x) 的值域正好是它的反函数y=f
-1(x) 的定义域（如下表）：
函数：y=f(x)；
反函数：y=f -1(x)；
定义域： A，C；
值域： C，A；
若确定函数y=f(x) 的映射f是函数的定义域到值域上的“一一映射”，那么由f的“逆”映射f
-1所确定的函数y=f
-1(x) 就叫做函数y=f(x) 的反函数. 反函数y=f
-1(x) 的
定义域、
值域分别对应原函数y=f(x) 的值域、定义域.。开始的两个例子：s=vt记为f(t)=vt,则它的反函数就可以写为f
-1(s)=s/v，同样y=2x+6记为f(x) =2x+6，则它的反函数为：f
-1(x) =x/2-3.
有时是反函数需要进行分类讨论，如：f(x) =x+1/x，需将x进行分类讨论：在x大于0时的情况，x小于0的情况，多是要注意的。
一般分数函数y=(ax+b)/(cx+d)（其中ad≠bc）的反函数可以表示为y=(b-dx)/(cx-a)，这可以通过简单的四则运算来证明。
[1]
参考资料
-
-
1.
课程教材研究所，中学数学课程教材研究开发中心编 ．人教版A版高中数学必修一：人民教育出版社 ，2007
-
2.
同济大学数学系．高等数学（第六版上册）．北京：高等教育出版社，2007：90
问题 ？
请发到 论坛
参阅
- 数学 - 数学符号 - 数学索引
- 手册 = 初中数学手册 + 高中数学手册 + 数学手册 + 实用数学手册
- 初等数学 = 小学数学 + 中学数学
( 初中数学 + 高中数学 )
- 高等数学 = 基础数学 ( 代数 + 几何 + 分析 ) + 应用数学
- 公式 - 定理 - 图
- 函数图 - 曲线图 - 平面图 - 立体图 - 动画 - 画画
- 书单 = 数学 + 物理 + 化学 +
计算 + 医学 + 英语 + 教材 - QQ群下载书
- 数学手册计算器 = 数学 +
手册 + 计算器 + 计算机代数系统
- 检测 - 例题 :
