§3 无条件极值问题解法

本节讨论目标函数

的极小值问题。设

[最速下降法]  迭代程序如下:

(1)       选取初始点及判别收敛的正数。

(2)       命

(3)       计算

(4)       命,若,则迭代停止,即为所求;否则进行(5)。

(5)       求,使

(6)       命;命,进行(3)。

这个方法虽然很简单，但点列收敛于最优解的速度较慢。

[牛顿法]  迭代程序如下：

(1)       选取初始点及判别收敛的正数。

(2)       命

(3)       计算。

(4)       命

若则迭代停止,即为所求;否则进行(5)。

(5)  求使

(6)  命;命,进行(3)。

牛顿法虽然可以很快地收敛于最优解,但往往计算逆矩阵很困难。为了避免此困难,产生了收敛速度介于最速下降法与牛顿法之间的共轭梯度法。

[共轭梯度法]

1^o  目标函数是二次函数

的情形,其迭代程序如下:

(1)  选取初始点及判别收敛的正数,若,则迭代停止;否则进行(2)。

(2)       命,

(3)       算出

(4)       命

(5)       若,则迭代停止;否则命

命,进行(3)。

对二次函数只要有限步就可到达最优点。

2^o  目标函数是一般函数的情形,其迭代程序如下:

(1)  选取初始点及判别收敛的正数。若,则迭代停止;否则进行(2)。

(2)  命,。

(3)  求使

(4)  命

(5)  若,则迭代停止;否则,若,则,进行(1),若,则算出

命                          

命,进行(3)。

这个方法的程序较简单,存储量较小,但当较小时,计算可能引起因舍入误差较大而不稳定的情况。

对一般(非二次)函数,这个方法不一定是有限步到达最优解。

[变尺度方法]

1°  目标函数是二次正定函数

的情形,其迭代程序如下:

(1)       选取初始点及判别收敛的正数。若,则迭代停止;否则进行(2)。

(2)       命,(阶单位矩阵),。

(3)       命。

(4)       算出

(5)       命

(6)       若,则迭代停止;否则,命

算出

再进行(7)。

(7)       命进行(3)。

对二次函数只要有限步就可到达最优点。

2°  目标函数是一般函数的情形,其迭代程序如下:

(1)       选取初始点及判别收敛的正数。若,则迭代停止;否则进行(2)。

(2)       命,,(阶单位矩阵)。

(3)       命。

(4)       求,使。

(5)      命。

(6)      若,则迭代停止;否则,若,则,进行(1),若,则算出

,,

命,进行(3)。

对一般(非二次)函数,这个方法不一定是有限步到达最优解。

变尺度法是共轭梯度法的改进,它的收敛速度较快。

[高斯-牛顿最小二乘法]  假设目标函数是平方和的形式

   

式中为维列矢量。

这是数据处理中最常见的一种函数形式。

显然,如果的极小点满足 (是预先给定的精度),那末可以认为是方程组

 

的解。所以最小二乘法也可用来求非线性方程组的解。

函数一般是非线性的,假设有连续的一阶偏导数:

  

迭代程序如下:

(1)       选择一初始点。

(2)       算出

式中

称为对初始值的校正量;又

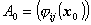
假设矩阵的列矢量为线性独立的,因此逆矩阵存在。

(3)       命

则为函数的极小点的首次近似。

(4)       以代替前面的,代替,重复上述计算过程,直到

或

为止,在此和为预先指定的表示对精确度要求的两个正数。

[改进的高斯-牛顿最小二乘法]  上述高斯-牛顿最小二乘法利用了目标函数为平方和的特点,用近似代替牛顿法中的二阶导数矩阵,大大节省了计算量,但是它对初始点的要求比较严格,如果初始点与极小点相距太远,这个算法往往失败。其原因可以从两个方面来看,其一是上述算法基于线性逼近,但在远离极小点时,这种线性逼近无效;其二是的最大特征值与最小特征值的比很大,以致使解变得无意义。为此采取下述改进的办法。

在求出的校正量后,不把作为第次近似,而将作为下一步的搜索方向,这时求使

极小值

然后令

以代替重复上述过程,直到

或                                 

时为止,这时极小点和极小值分别为

,

称为第步的最优步长因子。