|
图 7.28 |
九、曲面曲线的测地曲率、测地线与测地坐标
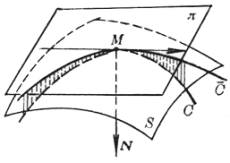
[测地曲率与贝尔特拉米公式] 设M为曲面S上一点,C为S上通过点M的一条曲线,![]() 为S在M的切面,
为S在M的切面,![]() 为C在
为C在![]() 上的正射影,则
上的正射影,则![]() 在M的曲率称为C在M的测地曲率,记作
在M的曲率称为C在M的测地曲率,记作![]() .
.
设曲面S的参数方程为![]() ,曲面曲线C的方程为
,曲面曲线C的方程为![]() ,则C的测地曲率
,则C的测地曲率
(1)
式中 ![]()
![]()
如果曲线C以弧长s为参数,则
(2)
式中 ![]()
![]()
公式(1)和(2)称为测地曲率的贝尔特拉米公式.
测地曲率是等距不变量.
[测地线] 如果一条曲面曲线C上每点的测地曲率都等于零,则称C为曲面上的一条测地线.
测地线的微分方程是
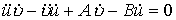
也可写为
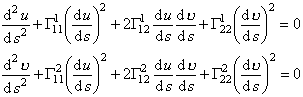
或
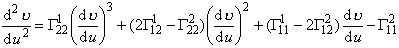
对于曲面![]() 上的测地线的微分方程为
上的测地线的微分方程为
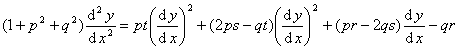
式中p,q,r,s,t 见前表.
测地线具有性质:
1、测地线在每点M的曲率小于与它在M相切的任何曲线在M的曲率.
2、如果把曲面曲线C的可展曲面变成平面时,那末只有测地线所对应的曲线是直线.
3、一条曲面曲线C是测地线的充分必要条件是:在C上每点的主法线与该点的曲面法线重合,即C的密切面包含曲面法线.
4、如果两个曲面沿一共同曲线C相切,假设C是其中一个曲面的测地线,则C也是另一个曲面的测地线.
5、通过曲面上每点沿每一方向有一条且有一条测地线.
6、在充分小的邻域里,测地线是短程线,即连接曲面上两个邻近点的一切曲面曲线中,测地线的长度最短.
[测地坐标] 若取坐标线u=常数为测地线![]() =常数的正交轨线,则称
=常数的正交轨线,则称![]() 为测地坐标,这族正交轨线称为测地平行线,这时
为测地坐标,这族正交轨线称为测地平行线,这时
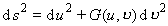
以测地坐标表示的总曲率为
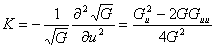
若测地线![]() =常数交于一点O,
=常数交于一点O,![]() 表示测地线
表示测地线![]() 和测地线
和测地线![]() 的交角,则称
的交角,则称![]() 为测地极坐标,这时的测地平行线称为测地圆,其半径等于u.
为测地极坐标,这时的测地平行线称为测地圆,其半径等于u.
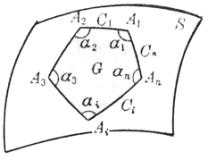
[高涅-波恩涅公式] 设G为曲面S上一个单连通区域,G的边界C是一条逐段光滑并无自交点的闭曲线,其运行的方向是使G总是在它的左侧.
|
图 7.29 |
设![]() 表示曲线C上任一点的测地曲率,
表示曲线C上任一点的测地曲率,![]() 为曲面面积元素,
为曲面面积元素,![]() 分别为C的角点
分别为C的角点![]() 的内角(图
的内角(图![]() ),则在G上的二重积分
),则在G上的二重积分
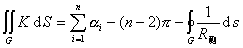
这称为高斯-波恩涅公式.特别
1、如果C是一条正则曲线(即无角点),这时![]() ,则
,则
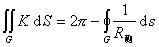

2、如果C是由n条测地线![]() 组成的测地多角形,这时(因
组成的测地多角形,这时(因![]() =0)
=0)
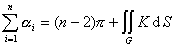
当![]() 时,C为三条测地线组成的测地三角形,这时
时,C为三条测地线组成的测地三角形,这时
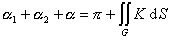
因次,![]() 的曲面上的测地三角形三内角之和大于
的曲面上的测地三角形三内角之和大于![]() ;
;![]() 的曲面上测地三角形三内角之和小于
的曲面上测地三角形三内角之和小于![]() ;
;![]() 的曲面上测地三角形三内角之和等于
的曲面上测地三角形三内角之和等于![]() .
.