§7 泛函分析初步
一、勒贝格积分
1、 测度与可测函数
[测度与可测集] 设S为某一区间![]() 内的任一有界点集,则把覆盖S的一组区间的长度之和的下确界称为S的外测度,记作
内的任一有界点集,则把覆盖S的一组区间的长度之和的下确界称为S的外测度,记作![]() .
包含S的任一有界区间
.
包含S的任一有界区间![]() 的长度
的长度![]() 与S关于
与S关于![]() 的余集(即
的余集(即![]() 内不属于S的点的全体)的外测度之差称为S的内测度,记作
内不属于S的点的全体)的外测度之差称为S的内测度,记作![]() .
.
![]() =
=![]() 的集S称为可测集,其测度记作
的集S称为可测集,其测度记作![]() .
.
设S为直线上的一个无界点集,若对一切大于零的x,![]() 是可测的,则称这个无界点集S是可测的. 在这种情形下,定义无界点集S的测度为
是可测的,则称这个无界点集S是可测的. 在这种情形下,定义无界点集S的测度为
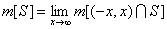
这里![]() 可以有限或无限.
可以有限或无限.
每个有界开集都是可测的.
可测集的概念可以推广到n维空间的点集上去.
[几乎处处] 若一个性质对区间上除了一个测度为零的集合之外,在其他点都成立,则称这个性质在已知区间上几乎处处成立.
[可测函数] 设函数![]() 在可测集S上定义,而c是任意实数. 若在S上使
在可测集S上定义,而c是任意实数. 若在S上使![]() 的一切点x所构成的集是可测的,则称函数
的一切点x所构成的集是可测的,则称函数![]() 为在S上的一个可测函数.
为在S上的一个可测函数.
在这个定义中,条件![]() 可用
可用![]() ,
,![]() ,
,![]() 中任一条件来代替.
中任一条件来代替.
在![]() 内任一连续函数是
内任一连续函数是![]() 内的可测函数.
内的可测函数.
若![]() 都是
都是![]() 内的可测函数,则
内的可测函数,则![]() (a为常数),
(a为常数),![]() 和
和![]() (极限存在)也都是
(极限存在)也都是![]() 内的可测函数.
内的可测函数.